Mixed-Precision Training of Deep Neural Networks
안녕하세요, 오늘은 NVIDIA Developer Blog 에 있는 Mixed-Precision Training of Deep Neural Networks 글을 바탕으로 Floating Point가 뭔지, Mixed Precision이 뭔지, 이걸 사용하면 어떠한 장점이 있는지 등을 정리해볼 예정입니다.
Floating Point
저희가 Deep Learning Model을 학습할 때 사용하는 대부분의 Framework 들은 기본적으로 32-bit Floating Point (FP32)로 학습을 시킵니다. 오늘 다룰 글에서는 Deep Learning Model을 FP32가 아닌 Mixed-Precision으로 학습시키는 과정을 다룰 예정인데요, Mixed Precision을 설명하기 전에 Floating Point에 대해 설명드리도록 하겠습니다.
Floating Point는 한글로는 부동 소수점이라 부르며 컴퓨터 공학을 배울때 기본적으로 배우는 개념입니다. 컴퓨터는 수를 이진법으로 표현하기 때문에 표현할 수 있는 숫자의 개수가 정해져있습니다. 예를 들어 비트가 4개가 있으면 총 2^4=16개의 수를 표현할 수 있는 셈이죠. 실수의 개수는 무한하기 때문에 컴퓨터에서 모든 실수를 완벽하게 표현할 수 없습니다. 그래서 나온 개념이 바로 Floating Point 입니다. 우리가 수를 나타낼 때 주로 십진법으로 나타내는데, 이를 이진법으로 바꿔서 표현한 뒤, 정규화 하며 2의 지수를 곱해 주는 형태로 변환합니다.
십진수 13.1875를 Floating Point로 표현하는 것을 예시로 들어보면, 우선 소수점 위의 부분인 13은 이진수로 나타내면 8 + 4 + 1 이므로 1101로 나타낼 수 있습니다. 소수점 아래 부분인 0.1875는 0.125 + 0.0625 이므로 0011 로 나타낼 수 있습니다. 즉 13.1875는 1101.0011 이며 정규화하면 1.1010011 x 2^3 로 나타낼 수 있습니다. 즉, 가수 (Fraction or Mantissa)는 1010011 에 남은 자리수는 다 0으로 채운 10100110000000000000000 로 나타낼 수 있습니다. 지수는 따로 부호 비트가 없어서 음수 값을 처리하기 위해 바이어스 표현법을 사용합니다. 0000000 이 -127을 의미하고 01111111이 0을, 11111111이 128을 의미합니다. 아까 구한 지수 값이 3 이었으므로 바이어스 표현법으로 나타내면 10000010 이 됩니다. 마지막으로 제일 앞에 붙는 부호 비트는 양수이므로 0이 되어서 최종적으로 01000001 01010011 00000000 00000000 로 나타낼 수 있게 되는 것입니다.
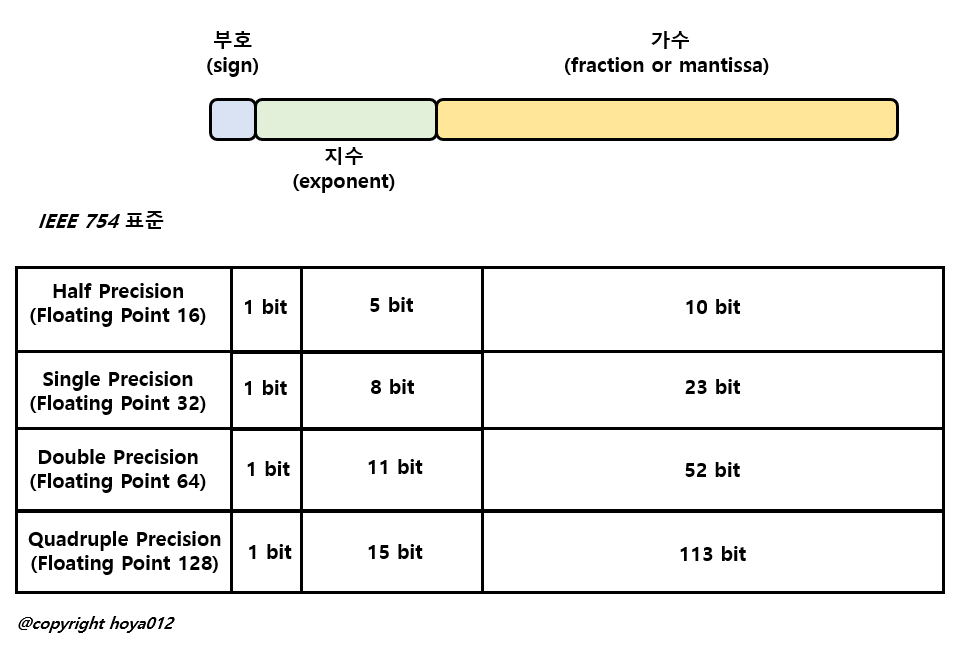
위의 그림은 IEEE 754 표준을 따르는 Floating Point 표기법을 나타낸 것이며, 주로 32-bit Floating Point를 사용하고, 이를 단 정밀도(Single Precision) Floating Point라 부릅니다. 더 세밀하게 수를 표현하기 위해 64bit를 사용하는 Double Precision 과 128bit를 사용하는 Quadruple Precision 도 사용되지만, 어떠한 방식을 사용해도 실수를 오차 없이 표현하는 것은 불가능 합니다. 반대로 더 적은 bit로 수를 표현할 때는 16bit을 사용하며, 이를 Half Precision이라 부릅니다.
대표적으로 0.1, 0.01, 파이(3.141592..) 등을 표현할 때 오차가 발생하고, 덧셈과 곱셈에서 결합 법칙, 분배법칙이 성립하지 않는 문제도 발생합니다. Floating Point로 실수를 근사하는 예시는 인터넷이나 컴퓨터 공학 책에서 잘 다루고 있으니 설명은 여기까지 하도록 하겠습니다.
Floating Point 를 이용한 Deep Neural Network
우선 저희는 일반적으로 Single Precision Floating Point를 사용하는데 최근 연구들을 보면 모델 사이즈가 점점 커지면서, 계산량과 필요한 메모리 크기 등이 기하 급수적으로 커지다 보니 학습을 시키기 위해 많은 리소스가 필요해지고, 학습, Inference도 오래 걸리는 문제가 발생합니다. 물론 거대 기업들은 수천, 수만개의 GPU를 이용하여 거대한 모델을 학습 시키겠지만 많은 비용이 발생하고 막대한 이산화탄소 배출로 인해 환경을 파괴하는 등 여러 문제가 뒤따라 발생합니다.
이러한 문제점에 주목하여 계산량을 줄이기 위해 딥러닝 모델의 학습에 Single Precision (FP32) 대신 Half Precision (FP16)을 사용하는 방법을 떠올립니다. Bit 수가 절반으로 줄어들어서 숫자를 표현할 수 있는 범위가 크게 줄어들었지만 계산량과 메모리 사용량을 크게 줄일 수 있겠죠?
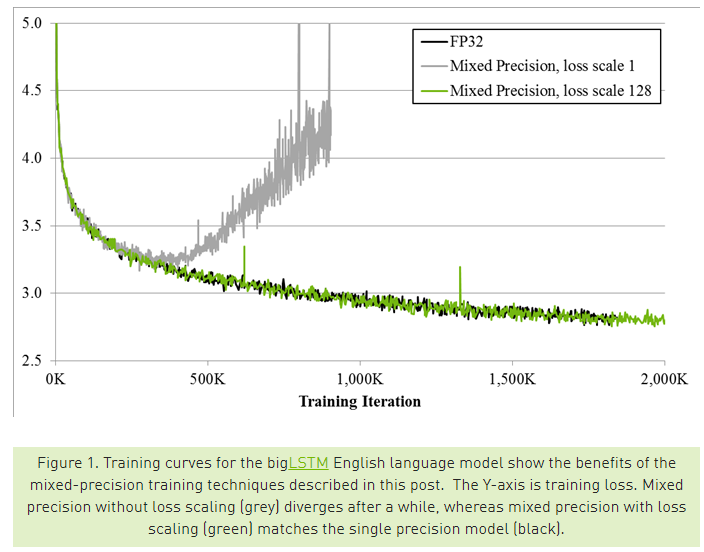
하지만 기존에 사용하던 코드에서 모든 값들을 FP32에서 FP16으로 바꿔서 학습을 시키면 training loss가 잘 떨어지다가 갑자기 증가하는 문제가 생기게 됩니다. 아무래도 학습을 하다 보면 back-propagation 과정에서 gradient를 계산하고 이를 acculmate 하여 weight를 업데이트 하는데, 이 과정에서 FP16은 표현할 수 있는 수의 범위가 좁다 보니 오차가 발생하고, 이 오차가 누적이 되면서 학습이 제대로 되지 않는 것입니다. 이러한 경향이 위의 그림에 잘 나타나고 있습니다. 위의 그림은 NVIDIA 블로그 글의 그림을 인용한 것인데요, 회색으로 그려진 loss graph가 별다른 처리를 하지 않았을 때의 학습 경향을 보여줍니다.
FP16이 실패하는 이유를 자세히 분석하면 다음과 같습니다. Half-Precision Floating Point는 앞서 설명드렸듯이 부호 1bit, 지수 5bit, 가수 10bit를 사용하는데, 이 때 지수가 표현할 수 있는 수의 범위는 [-14, 15] 이며, subnormal number (혹은 denormal number) 까지 고려하면 [-24, 15] 까지 표현할 수 있게 됩니다. 즉, [2^-24, 1.1111111111 x 2^15 =65,504] 범위의 수를 표현할 수 있는 것입니다.. [2^-149, 3.4x10^38] 의 범위의 수를 표현할 수 있는 Single Precision에 비해 굉장히 협소한 범위를 가지고 있기 때문에 당연히 학습 과정에서 gradient 값이 너무 크거나, 너무 작은 경우에 수를 제대로 표현하기 힘들어 집니다. 주로 gradient 값이 엄청 작은 경우에 문제가 발생합니다.
Mixed Precision Training
자, 이제 위에서 다룬 Floating Point 개념을 바탕으로 Mixed Precision 에 대해 설명드리도록 하겠습니다. NVIDIA와 Baidu Research 연구진들은 이러한 점을 해결하기 위해 Mixed-Precision Training 이라는 기법을 제안합니다. 이 논문은 2018 ICLR에서 발표가 된 논문입니다.
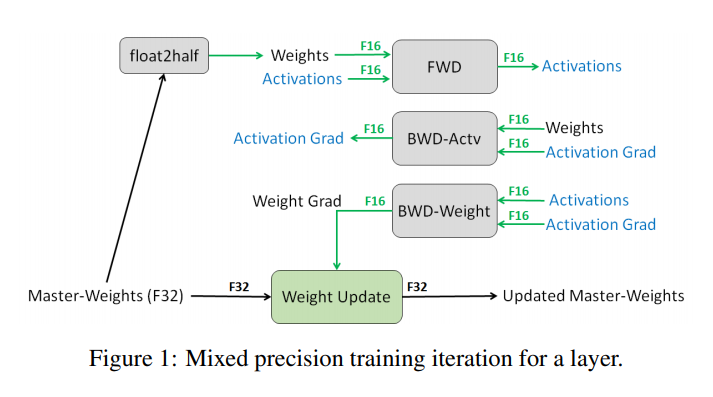
위의 그림은 논문의 서두에 등장하는 그림이며, Mixed-Precision Training의 핵심을 잘 보여주고 있습니다. 우선 Master-Weight를 FP32 에서 FP16 으로 변환한 뒤, Forward Propagation과 Backward Propagation은 모두 FP16으로 연산이 수행됩니다. 그 뒤, Weight를 Update하는 과정에서 다시 FP32로 변환이 되어 값이 축적되어 Weight가 업데이트가 됩니다. 이 과정에서 Loss Scaling 이라는 기법이 추가가 되는데, 그림을 통해 설명드리겠습니다.
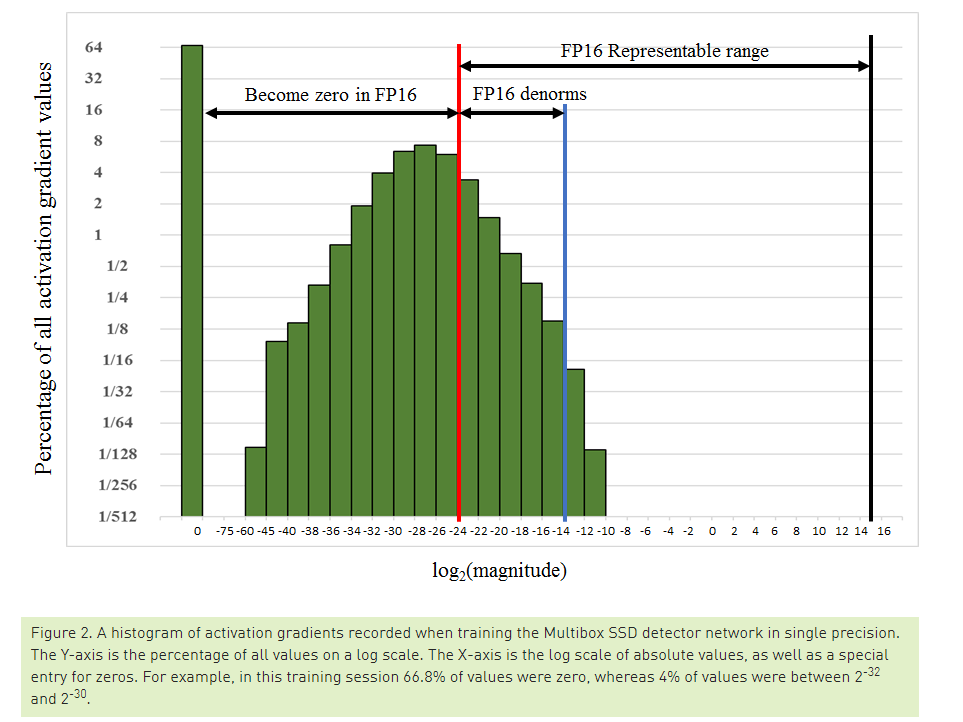
Deep Neural Network의 학습에 관여하는 Tensor는 총 4가지로 나눌 수 있습니다. Activations, Activation gradients, Weights, Weight gradients. 저자들이 FP16으로 학습을 시켰을 때, Weights와 Weights gradients는 FP16이 나타낼 수 있는 수의 범위 안에 잘 들어오는 편이었다고 합니다. 다만, 일부의 network에서 굉장히 크기가 작은 Activation gradients 값이 관찰되었고, FP16이 나타낼 수 있는 수의 최소 범위인 2^24 보다 작게 되어서 0으로 강제 변환이 되게 됩니다. 위의 그림은 SSD Object Detector를 학습시킬 때 Activation gradients들의 크기의 빈도를 히스토그램으로 나타낸 것입니다. 대부분의 gradient 값들이 FP16이 나타내지 못하는 구간에 존재하는 것을 확인할 수 있습니다.
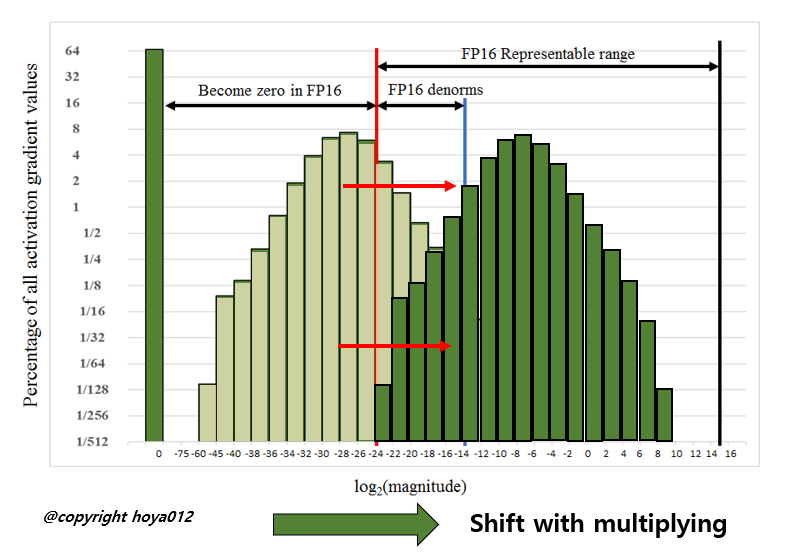
또한 FP16이 나타낼 수 있는 범위 중에 왼쪽 영역에 값들이 몰려있는데, 가장 쉽게 접근할 수 있는 생각은 이 값들을 오른쪽으로 밀어주는 것이죠. 즉, gradient에 큰 수를 곱해서 값들을 오른쪽으로 shift 시키는 아이디어입니다. 저자들은 간단하게 gradient 값들에 8을 곱해서 학습을 시켜보니 SSD 가 학습이 잘 되는 것을 확인하였습니다. 즉, 값이 작은 gradient 들을 모두 다 살릴 필요는 없고, 2^-27 ~ 2^-24 범위의 gradient만 잘 살려도 학습이 잘 되는 것을 관찰합니다.

NVIDIA 측에서 작성한 Training with Mixed Precision User Guide 문서에서는 처음엔 Scaling Factor를 큰 값으로 사용한 뒤에 점진적으로 값을 줄이고 늘리는 방식으로 적절한 값을 튜닝하는 것을 가이드로 제공하고 있습니다.
Mixed Precision Training 실험 결과
마지막으로, Mixed Precision으로 학습을 시켰을 때 정확도 손실이 어느정도 발생하는지를 다룬 실험 결과를 보여드리겠습니다. 저자들은 Classification, Object Detection, Speech Recognition, Machine Translation, Language Modeling, DCGAN 등 다양한 task에 대해 Mixed Precision을 적용하여 성능을 검증하였습니다.
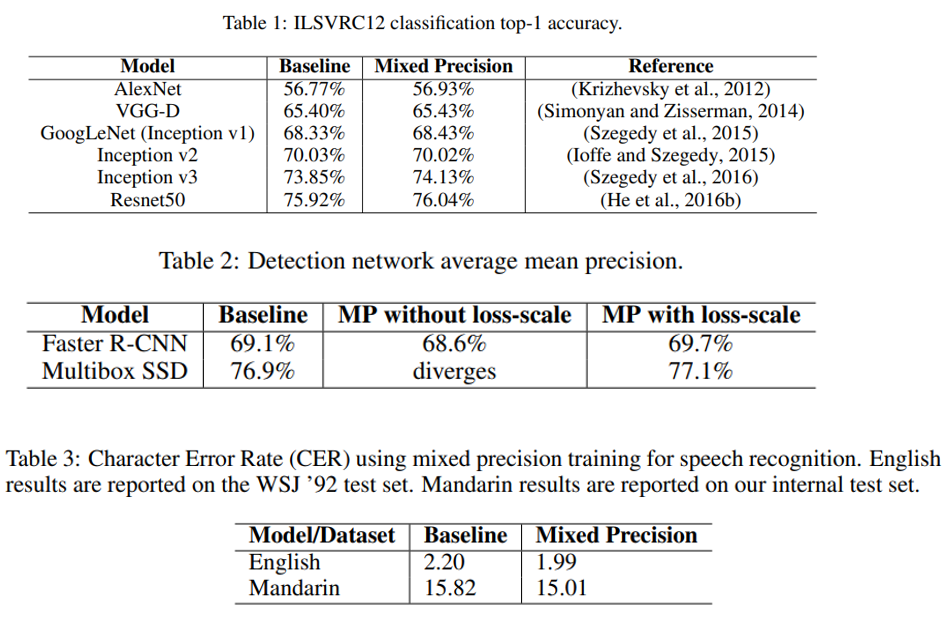
Classification 에는 ImageNet 데이터셋을 사용하였고 FP32를 사용하였을 때와 거의 유사하거나, 약간 오른 accuracy를 얻을 수 있었다고 합니다. 당연히 학습 시간도 빨라졌겠죠? 다만 동일한 하드웨어에서 학습 시간이 얼마나 줄어들었는 지에 대해선 언급하고 있지 않아서 결과가 궁금하네요.
Object Detection은 PASCAL VOC 2007에 대해서 Faster R-CNN과 Multibox SSD로 실험을 하였으며, SSD의 경우 loss-scaling을 하지 않으면 학습이 발산을 하였는데, 128배 loss scaling을 해주면 FP32와 거의 비슷한 성능을 얻을 수 있었다고 합니다.
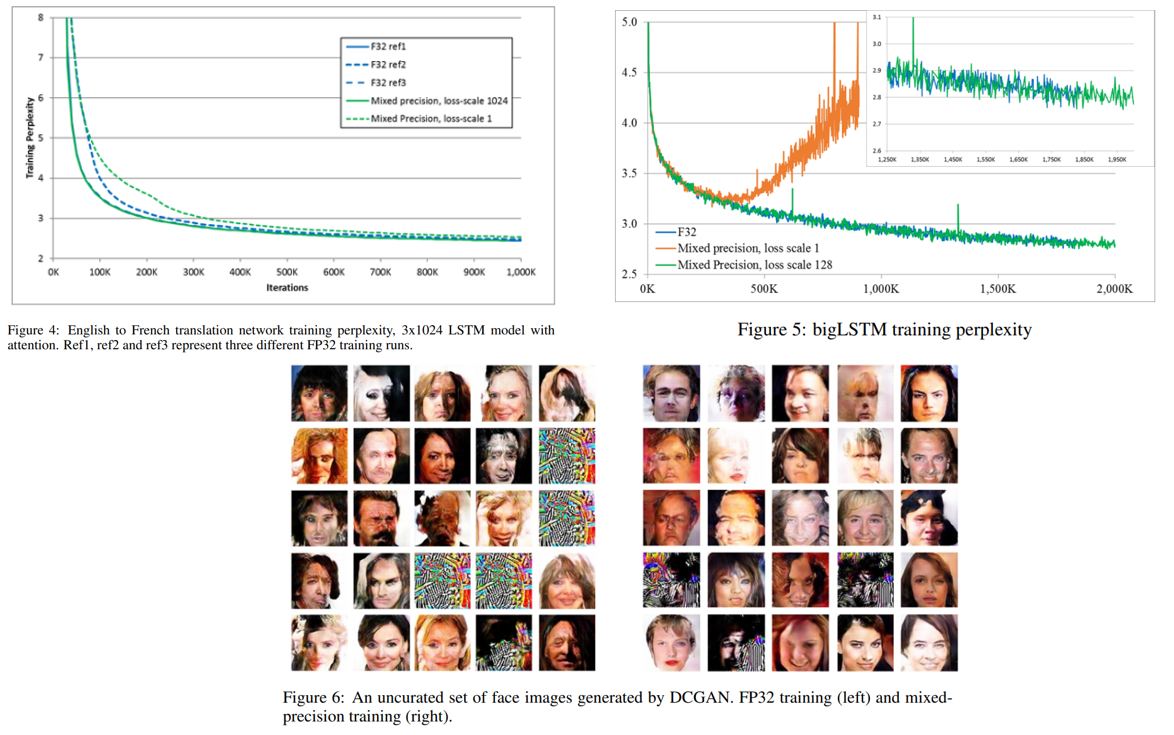
Computer Vision Task 뿐만 아니라 음성 인식, 기계 번역, Language Modeling, DCGAN을 이용한 이미지 생성 등 다양한 task에서도 성능이 잘 유지가 되는 것을 확인하실 수 있습니다.
NVIDIA GPU
오늘 다룬 Mixed Precision Training이 저희가 일반적으로 사용하는 NVIDIA GPU만 있으면 사용할 수 있는지 짧은 식견으로 정리를 해보았습니다. (틀린 내용이 있을 수 있습니다! ㅠㅠ 잘못된 내용이 있으면 정정 부탁드릴게요!)

우선 NVIDIA GPU에도 Intel의 CPU처럼 세대가 존재합니다. 제가 2018년 SIGGRAPH 학회에 갔을 때 Turing 아키텍처가 공개가 되었었는데, 올해 5월 NVIDIA의 GTC 2020 행사에서 Ampere 아키텍처가 공개되었습니다. 저는 주로 Pascal 아키텍처의 1080 Ti를 이용하고 있는데 이 GPU 에는 Tensor Core가 들어가 있지 않습니다. Tensor Core는 Pascal 다음 세대인 Volta에서 처음 도입되었습니다.
저는 Tensor Core가 없으면 Mixed Precision Training을 못 한다고 생각했는데 그건 아닌 것 같습니다. Tensor Core가 있으면 더 효과적으로 학습 시간을 가속할 수 있지만, Tensor Core가 없어도 Pascal 아키텍처와 CUDA 8 이상의 버전을 사용하면 Mixed Precision을 이용할 수 있는 것 같네요.
미디엄의 “RTX 2080Ti Vs GTX 1080Ti: fastai Mixed Precision training & comparisons on CIFAR-100” 글에서 Turing 아키텍처의 2080 Ti와 Pascal 아키텍처의 1080 Ti 에 대해서 FP32와 Mixed Precision으로 학습을 시켜 시간을 비교하였습니다. 제가 딱 궁금했던 부분을 긁어주는 글입니다. ㅎㅎ
제 우려와는 다르게 1080 Ti에서도 Mixed Precision Training을 하면 학습 시간이 단축이 되며, 모델의 크기가 클수록 가속되는 비율이 높아지는 경향을 보였습니다. 그리고 역시나 2080 Ti에서 더욱 효율적으로 학습 시간이 단축되는 경향을 보였다고 합니다.
아직 Mixed Precision Training을 직접 실험해보지 않아서 코드를 얼마나 바꿔야할 지 감은 안오지만, 여러 문서들에서는 몇 줄만 추가하면 쉽게 사용할 수 있다고 하니 조만간 사용을 해볼 예정입니다. 정확도가 유지되는데 학습 시간을 줄일 수 있고, Memory 사용량도 줄일 수 있다면 사용하지 않을 이유가 없겠죠?
결론
오늘 글에서는 NVIDIA 개발 블로그에 있는 Mixed Precision Training 글과 논문, 유저 가이드 문서를 바탕으로 Mixed Precision Training에 대해 정리를 해보았습니다. 또한, Mixed Precision을 이해하기 위해 먼저 Floating Point에 대해 잘 알고 있어야 하므로, Floating Point에 대해서도 설명을 드렸습니다.
또한 단순히 FP32에서 FP16으로 바꿔서 학습을 시키면 발생하는 문제와, 그 문제를 해결하기 위해 어떤 방법을 적용하였는지, 적용하였을 때 성능이 어떻게 좋아지는지 등을 정리해보았습니다. 잘 알아두면 굉장히 쏠쏠하게 사용할 수 있는 테크닉인만큼 저도 잘 숙지해둘 예정입니다. 다음 글에서는 최근 PyTorch 1.6에서 공식적으로 Mixed Precision Training을 지원한다고 하여, 해당 내용을 튜토리얼로 정리드릴 예정입니다. 읽어주셔서 감사합니다.