An introduction to entropy, cross entropy and KL divergence in machine learning
안녕하세요, 오늘은 머신러닝을 공부하다 보면 자주 듣게 되는 용어인 Cross entropy, KL divergence에 대해 알아볼 예정입니다. 이 개념을 잘 정리해 놓은 글 을 발견해서 이 글을 바탕으로 제 나름대로 번역하고 설명, 그림 등을 추가하여 설명드릴 예정입니다!
Information and Entropy
Information은 정보이론에서는 bit로 측정되며, 주어진 이벤트에서 발생하는 놀라움의 양 으로 이해할 수 있습니다. 엄청 불공평한 동전이 있다고 가정해봅시다. 앞면이 나올 확률이 99%, 뒷면이 나올 확률이 1%일때, 앞면이 나오는 일은 놀랍지 않습니다. 다만 뒷면이 나오면 굉장히 놀라겠죠. Information의 수학적 정의는 다음과 같습니다.
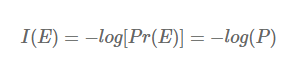
특정한 stochastic event E에 대한 확률의 negative log로 나타낼 수 있으며, 밑이 2인 로그를 사용합니다. 머신러닝에서는 종종 대안으로 자연로그 (nats)가 사용된다고 합니다. 무튼, 다시 동전 던지기로 넘어가서 앞면에 대한 information은 -log2(0.99) = 0.0144bits 로 굉장히 낮으며, 반대로 뒷면에 대한 information은 -log2(0.01) = 6.64bits 로 높은 값을 갖습니다. 즉, 놀라움의 정도가 information에 잘 반영되어 있죠.
자 이제 Entropy에 대한 설명을 시작하겠습니다. Entropy는 특정한 stochastic process에서 생성된 information의 평균! 즉, Information의 기대 값이며 위의 동전 예시를 통해 Entropy H(X)를 구해보면 다음과 같습니다.

즉, 불공평한 동전은 0.08bits의 평균 정보 전달률을 갖는 stochastic information generator인 셈입니다. 공평한 동전(앞면 뒷면 각각 0.5)에 대해서 계산을 해보면 -(0.5 x -1 + 0.5 x -1) = 1bit가 나옵니다. 어떻게 보면, 불공평한 동전은 결과값을 예측하기 굉장히 쉬워서 Entropy 값이 낮게 나왔고, 공평한 동전은 결과값을 예측하는 게 굉장히 어렵기 때문에 Entropy 값이 높게 나온 셈이죠.
Entropy and Machine Learning
위의 설명을 통해 Entropy의 정의를 알게 되었습니다. 이제 Entropy가 머신러닝에서 어떻게 사용되는지 알아볼 차례입니다. 머신러닝을 다뤄봤다면 Cross-Entropy는 한 번쯤은 들어봤을 것입니다. 이건 밑에서 더 자세히 다룰 예정이고, 그냥 Entropy도 머신러닝에서 자주 사용됩니다. 강화학습의 policy gradient optimization을 예로 들면, Neural Network는 agent를 control하도록 학습되고, NN의 output은 softmax layer로 구성되어 있습니다. 이 softmax output layer는 agent가 취할 수 있는 best action의 확률 분포 형태를 띄는데, 만약 action size 4를 갖는 environment가 있으면 output은 주어진 game state에 대해 다음과 같이 나타날 수 있습니다. (예시입니다)
- {0.9, 0.05, 0.025, 0.025}
위와 같은 경우 agent는 아마도 첫번째 action을 선택할 것입니다. 하지만, 강화학습에서 고려되어야 하는 요소에 “agent가 특정한 하나의 action 혹은 strategy에 너무 빠르게 수렴하면 안된다!” 는 조건이 있습니다. 이를 encouraging exploration이라 부릅니다. Policy gradient에서는 exploration은 output layer의 entropy의 negative를 loss function에 녹여 냄으로써 위의 조건이 만족됩니다.
위의 예시로 든 output에서 첫번째 action(p=0.9)을 선택을 고려한 entropy는 매우 낮습니다.
- (0.9 x log2(0.9) + 0.05 x log2(0.05) + 0.025 x log2(0.025) + 0.025 x log2(0.025)) = 0.61bits
만약 softmax layer의 output이 {0.3, 0.2, 0.25, 0.25} 형태였으면 entropy는 1.98bits로 거의 3배가 됩니다. 즉, agent가 어떤 action을 취해야 할지에 대한 불확실성이 더 커진 셈이며, 불확실성이 entropy에 반영됩니다. Negative entropy가 loss function에 반영이 되어 있다면, 높은 entropy 값은 낮은 entropy 값보다 loss를 더 크게 줄일 것이며, 그 덕에 특정 action에 너무 빠르게 수렴하는 것을 방지해줄 것입니다. Entropy는 머신러닝에서 강화학습 외에도 Bayesian methods에서도 주로 사용되지만 오늘 글에서는 다루지 않을 것입니다.
Cross entropy and KL divergence
자, 이제 Cross entropy를 다뤄보겠습니다. Cross entropy는 두 확률 분포 P, Q 사이의 차이를 측정하는 지표입니다. 위에서 다룬 entropy는 하나의 확률 분포에 대한 측정 지표였다면, Cross entropy는 두 확률 분포에 대한 측정 지표인 셈이죠. 머신러닝에서 주로 사용되는 neural network에 대해 생각해보면, supervised learning 셋팅에서 GT가 존재하기 때문에 true probability distribution P가 존재하고, neural network가 학습을 통해 approximate probability distribution Q를 배우게 됩니다. 이 때, P와 Q 사이의 거리 혹은 차이를 최소화할 필요가 있습니다. 아래 그림은 cross entropy 함수의 정의입니다.
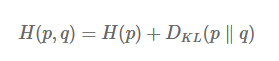
첫번째 term은 true probability distribution p의 entropy를 의미하고, optimization 동안 고정되어 있고, optimization 과정에서 approximation probability distribution q가 바뀌며 이에 따라 두번째 term이 바뀝니다. 이 두번째 term에서 분포 P와 분포 Q의 정보량의 차이가 정의됩니다. 즉, 두 확률 분포의 차이를 나타내는 지표인 cross entropy의 핵심은 두번째 term인 KL divergence입니다. 이제 KL divergence가 뭔 지 설명 드리겠습니다.
KL divergence
두 확률 분포 간의 KL divergence는 정보 이론적인 관점에서 보면 굉장히 다양한 해석이 가능하며, “놀라움”의 표현이기도 합니다. 두 확률 분포 P, Q가 가까웠다는 가정 하에, 만약 P와 Q가 가깝지 않다면 놀라운 일이며, 이 때 KL divergence는 높은 값을 갖게 되며, 반대로 가정대로 P와 Q가 가깝다면, 이는 놀랍지 않은 일이며 KL divergence도 낮은 값을 갖게 됩니다.
Bayesian 관점에서 보면 KL divergence는 prior distribution Q에서 posterior distribution P로 이동할 때 얻어지는 information을 의미합니다. KL divergence의 표현은 likelihood ratio approach를 통해 나타낼 수 있습니다. likelihood ratio는 아래와 같이 쉽게 표현이 가능합니다.
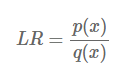
만약 어떠한 값 x가 임의의 분포로부터 sampling 되었을 때, likelihood ratio는 sample이 분포 q보다 분포 p에서 나왔을 확률을 의미합니다. p에서 나왔을 가능성이 높은 경우 LR은 1보다 큰 값을 갖고, 반대의 경우 1보다 작은 값을 갖습니다. 독립적인 sample이 많이 있고, 이 모든 것들을 고려하여 likelihood function을 추정한다고 가정해봅시다. 그러면 아래와 같이 LR을 나타낼 수 있습니다.
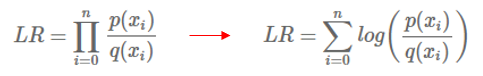
왼쪽 식을 ratio에서 log를 씌워주면 오른쪽과 같은 식을 얻을 수 있습니다. log 내부에서는 곱셈이 합으로 바뀌게 되죠. 이를 log likelihood ratio라 부릅니다. 이제 우리는 likelihood ratio를 모종의 합으로 표현할 수 있게 되었습니다. 이제 각 sample들이 평균적으로 q(x)보다 p(x)에서 나왔는지를 정량화 하는지에 대해 답해봅시다. 답하기 위해 우리는 likelihood ratio에 기대값을 취할 것입니다.
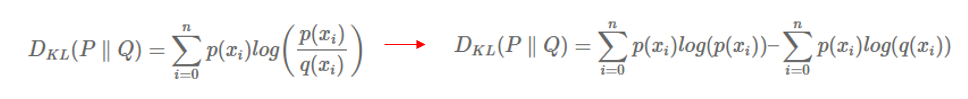
이렇게 log likelihood ratio에 기대값을 취해준 값이 바로 KL divergence 입니다. 즉, 정리하면 KL divergence는 얼마나 sampled data가 Q 분포 대신 P 분포로부터 나왔는지를 나타내는 likelihood ratio의 기대값입니다! 정리가 잘 되셨나요?
KL divergence를 나타내는 방식에는 왼쪽 그림도 자주 사용되고, log를 전개한 오른쪽 그림도 자주 사용됩니다. 오른쪽 그림의 첫번째 term은 P 분포에 대한 entropy를 의미합니다. 위의 entropy 설명 부분을 보시면 식이 정확히 일치하며, entropy는 information의 기대값을 의미 했었죠. 식의 두번째 term은 뭔가 Q 분포에 대한 entropy를 나타내는 것 같지만, 자세히 들여다보면 q(x)가 아닌 p(x)가 곱해져 있습니다. 즉, P 분포에 의해 weighted 되어서 계산이 됩니다.
이를 해석해보면, 만약 P가 true distribution인 경우에 KL divergence는 Q를 통해 표현할 때 손실된 정보의 양을 의미합니다. 어렵죠? 사실 저도 잘 와 닿지 않습니다. 추상적으로 생각해보면, 만약 P 분포와 Q 분포가 거의 같은 분포였다면, P를 Q로 나타내도 정보의 손실이 거의 발생하지 않을 것입니다. 하지만 두 분포가 차이가 있었다면 P를 Q로 나타내는 과정에서 정보가 손실이 될 것이며, 이를 수식적으로 나타낸 값이 위의 식입니다.
KL divergence의 가장 중요한 특징은 교환법칙이 성립하지 않는다는 점입니다.
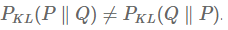
즉, P와 Q의 KL divergence는 Q와 P의 KL divergence와 다른 값을 가집니다. 즉, KL divergence는 두 분포 간의 거리 개념이 아니며 distance metric도 아닙니다.
Cross entropy
위에서 정의했던 Cross entropy 함수를 다시 들여다보면, P와 Q의 Cross entropy는 true distribution P의 entropy와, P와 Q의 KL divergence의 합으로 정의가 되어있습니다. 그리고 KL divergence도 위에서 식을 유도 했었죠. 이 두 term을 더하면 Cross entropy를 아래와 같은 식으로 나타낼 수 있습니다.
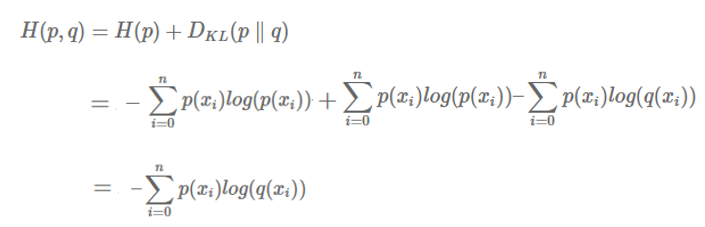
이 식은 다들 친숙하실 것입니다. 주로 classification 문제를 풀 때 cross entropy loss를 사용하죠. 주로 true distribution P로는 one-hot encoded vector를 사용합니다. 예를 들어 0~9까지 손으로 쓴 숫자를 분류하는 MNIST classification에서 숫자 2의 경우 true distribution (GT)은 {0, 0, 1, 0, 0, 0, 0, 0, 0, 0}이 됩니다.
그리고 우리가 설계한 neural network의 output layer에 보통 classification의 경우 softmax layer를 마지막에 붙여줘서 output 값들이 0~1사이의 확률 값이 되고 다 더하면 1이 되도록 만들어줍니다. 제가 설계한 neural network가 숫자 2 이미지를 다음과 같이 예측했다고 가정해봅시다.
- Q = {0.01, 0.02, 0.75, 0.05, 0.02, 0.1, 0.001, 0.02, 0.009, 0.02}
neural network가 예측한 Q와 P의 차이를 측정하려면 어떻게 하면 좋을까요? 두 확률 분포 간의 차이를 측정하는 지표, 바로 Cross entropy를 사용하면 됩니다. P는 이미 one-hot encoding이 되어있기 때문에 2번째 값을 제외하면 모두 0 값을 갖게 됩니다. 이렇게 P가 one-hot encoding 되어있는 경우 Cross entropy는 시그마를 사용하지 않고 나타낼 수 있습니다.
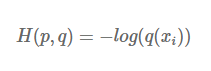
위의 예시를 보면 Cross entropy loss는 -log(0.75) = 0.287 값을 갖게 됩니다. log 그래프를 떠올려보면, Q 값이 1에 가까워질수록 loss는 감소하다가 0으로 가겠죠? 이런 식으로 classification 문제에서 Cross entropy loss가 사용이 되고 있습니다. 이렇게 Cross entropy를 최소화하면서 neural network를 학습시키게 되는데, 이 Cross entropy 식 자체가 P에 대한 Entropy와 P, Q간의 KL divergence의 합으로 구성이 되어있기 때문에 어떻게 보면 KL divergence를 최소화하는 것과 같습니다.
정리하면, Cross entropy와 KL divergence는 밀접한 관계를 가지고 있으며, 각각이 가지고 있는 특징들을 잘 기억해두시길 권장 드립니다.
결론
이번 포스팅에서는 잘 정리가 된 문서를 바탕으로 Entropy, KL divergence, Cross entropy 등을 정리해보았습니다. 다소 헷갈리는 개념들이 많아서 한 번 더 요약을 하겠습니다.
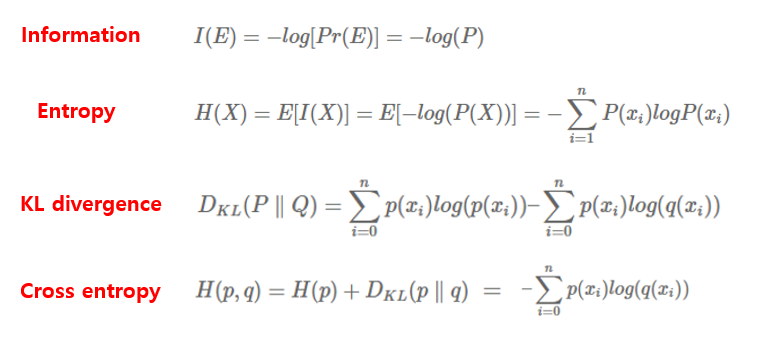
- Information: 주어진 임의의 이벤트에서 발생하는 놀라움의 양
- Entropy: 주어진 임의의 이벤트에서 발생한 Information들의 기대값
- KL divergence: 두 확률 분포 P, Q가 있을 때, P 분포를 근사하는 Q 분포를 통해 샘플링할 때 발생하는 정보량의 손실
- Cross entropy: 두 확률 분포 P, Q 사이의 차이를 측정하는 지표
정보이론을 깊게 알진 못해서 제 나름대로 짧은 식견을 통해 정리해보았는데요, 혹시 틀린 내용이 있거나 궁금하신 점이 있으면 댓글에 꼭 남겨 주시면 감사드리겠습니다!